Dimensional and Hyper-Dimensional Logics

This post combines several notes about a new kind of logic.

Roughly, I'm guided by the following kind of thinking: consider a scenario where Bob and Bill are fighting about what to buy. Bob and Bill spend hours, days even arguing about how to spend their dwindling resources. Beatrice enters the debate and swiftly points out that if they simply got new jobs or took out a loan, they wouldn't have to fight at all.

Normally, we might be quick to chalk the scenario above up to some vague notion of "practical intelligence" (practicality) or "knowledge". What if it's more about the kind of thinking employed?

Part of my motivation is to capture a kind of thinking that's traditionally been considered by Hegelians and those in the field of formal rhetoric (so-called informal logics and perhaps most-prominently developed by Rescher). These logics are:

1. Defeasible (non-monotonic) - that is, open to evidence - the conclusions can be altered by new information.
2. Dynamic and real-time - Boolean Algebra is a system of fixed truths and tautologies that are unalterable.
3. Depend on human interactions like a debate, a legal conflict, etc.

These systems are also usually adversarial and dialogical (involving the arguments of multiple people) in some kind of social activity [game] with a decision procedure to determine a victor.

These informal logic systems are also usually explicitly introduced as non-exhaustive. They don't claim to be a "complete" system or description. (Classical Logic and its isomorphic brethren are sound and complete which therefore express all possible tautologies of Classical Logic. They are "total" in this sense.)

Are there ways to supplement existing thinking systems to improve the outcome of a debate, adversarial contests, or strategic thinking?

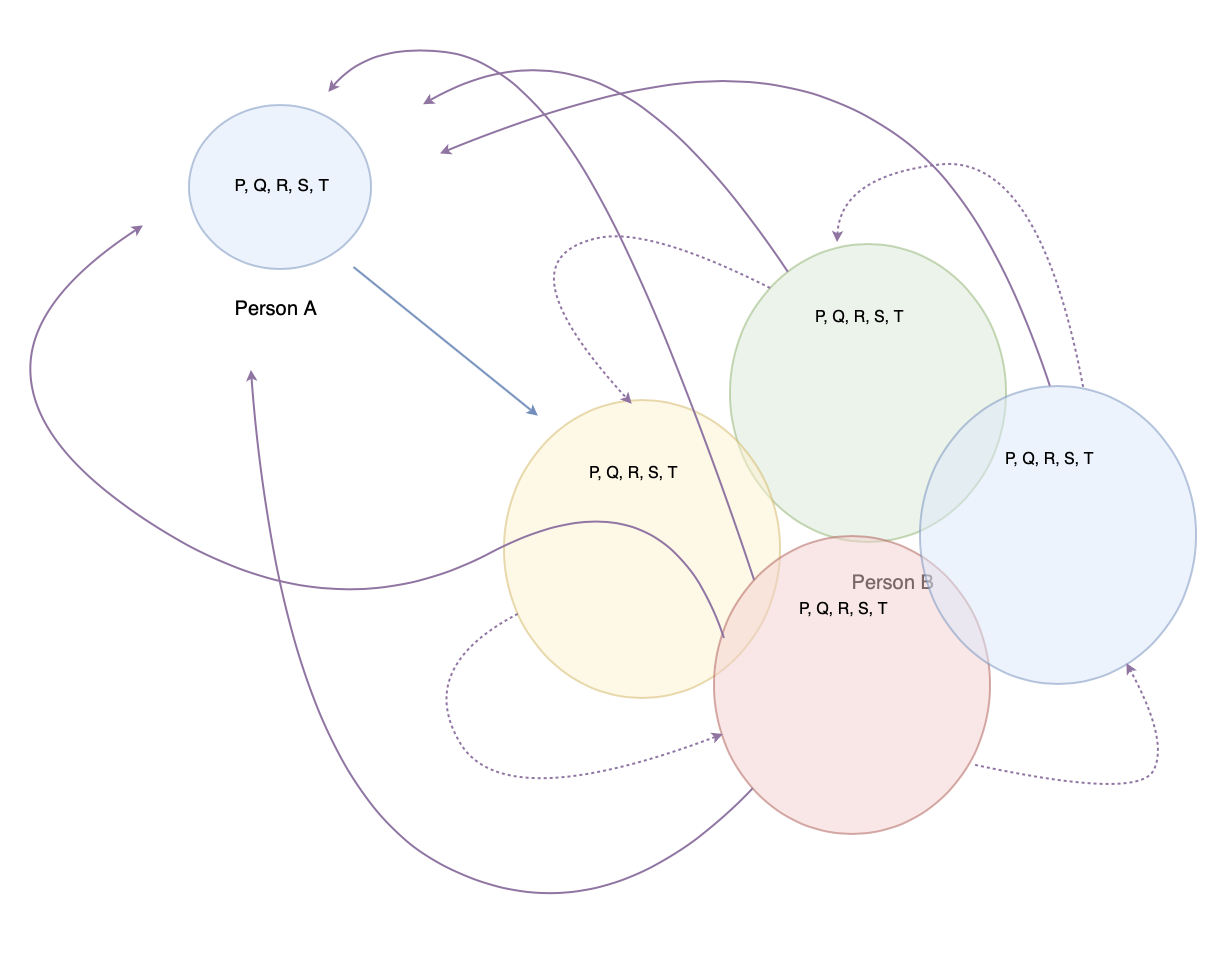
Precursors

Some historical precursors.

Frege's Begriffsschrift (Thinking Notation)

Frege introduced the first predicate logic notation vastly expanding the semantic power of logic from its sentential moorings.

He introduced:

1. Existential quantification.
2. Universal quantification.
3. Predicates.
4. Identity.

His original formulation was very ambitious for its time and he was unnecessarily self-critical about its success when it was discovered to be contradictory.

At that time, no predicate logic yet existed so, the distinction between First-Order and Second-Order logics hadn't yet been made.

Second-Order logic continues to have a more dubious reputation than First-Order logic (which is provably sound and complete). It has been suggested (by Quine for instance) that Second-Order logic may, in fact, be identical to (or a fragment of) Set Theory since it involves quantification over predicates (and not just objects).

Peirce's Existential Graphs

Peirce and Boole were among the first two logicians that are usually credited with formulating symbolic logic. That is, taking the ancient and archaic syllogistic square from Aristotle and presenting a mathematically rigorous definition for logic.

Pierce, like Frege, developed a logical system that may strike us as peculiar today given the use of symbolic tokens (of a formal language). He basically invented the first theory of Venn Diagrams and showed how operations could be evaluated using spatial concepts.

Venn's Diagrams

Venn Diagrams are fairly ubiquitous and are used to teach set theory.

One way many college students are taught Boolean Algebra is through Venn Diagrams. That practice continues today with respect to SQL Join operations.

Hilbert Space Formalisms of Quantum Logic

Some Quantum Logical formulations involve the use of mathematically rigorous spatial concepts (like Hilbert Space). Here, propositions are defined as physical interactions within that space.

Spencer-Brown's Laws of Form

Spencer-Brown's famous Laws of Form goes back to the most basic concepts in an attempt to elucidate a classical theory of logic. It's easy to prove that the system he discovered is isomorphic to classical logic (pretty rad!).

Schwerpunkt

Not a mathematical term but an admitted inspiration. Shwerpunkt is a military concept about avoiding difficult geographic and spatial obstacles (like fortifications or river crossings). Historically (and by nature), humans attempt to identify major problems and tend to gravitate towards them drawing resources into their attempts to resolve them.

Shwerpunkt (literally, "the hard place" or "focal point") is the deliberate identification of these pain points and the attempt to move around them.

In the example above, Bill and Bob are debating how to use their money. One might think that the pain point is the money itself (or the other person in the argument). However, Beatrice correctly identifies a better way to work around those obstacles that involves less cost and provides a potential solution. She might say that the problem point is the argument itself rather than the participants (in both senses: the components of the debate and Bill and Bob) to it.

Here, I am motivated to develop a framework to define "thinking around" certain propositions.

Spatial Logics

So, we can generalize those notions and potentially link some of these thoughts to evolving considerations in Univalent Foundations.

Some New Ideas

Truth-conditions are well-understood but few systems have talked much about these can be expanded or compressed.

This is not a superfluous exercise - consider standard Modal Logical semantics which involve complex truth-conditions defined within a world frame.

Logical Dimension

We might think of truth-conditions as a set of determinations for the assignment of truth-values. (And, interpretation functions as just the assignment according to those specified conditions.)

A criterion of evaluation. For example, a world-frame condition (e.g. - p is true at w). Another would be a truth-value of Classical Logic.

We can think about Boolean semantics as being one-dimensioned (since it concerns the assignment of T or F.). As noted, other logics have more complex semantical machinery which involves other considerations (occasion of utterance, context, world, or universe, etc.).

I think this is fair. When we think of a dimension here, w.r.t. semantics, the dimension involves just the kinds of judgements we are trying to regiment our system of thinking by. Thus, in Boolean Algebra we are concerned with Truth (solely) but in Modal Logic we are concerned with Truths-at-Worlds.

Lower-Dimensional Logics

One Dimensional Logic (not to be confused with predicate quantification or so called higher-order logics):

1. One layer - layer approach pertains to the number of wrapping logics
2. {T, F} or {0, 1} - one criterion for semantic evaluation

Two Dimensional Logic:

1. Two layers (one wrapping) e.g. - convenient rewriting of Meta and Object language relationships
2. ({T, F} or {0, 1}) and V e.g. - two requirements for truth-aptness. More stringent truth-conditions

Higher-Dimensional Logics

N-dimensional truth-conditions.

Dimensional Hierarchies

A Dimensional Hierarchy is at least two logics L1, L2 such that:

1. The truth-values of L1 are a subset of the truth-values of L2.
2. The truth-conditions of L1 are a subset of the truth-conditions of L2.

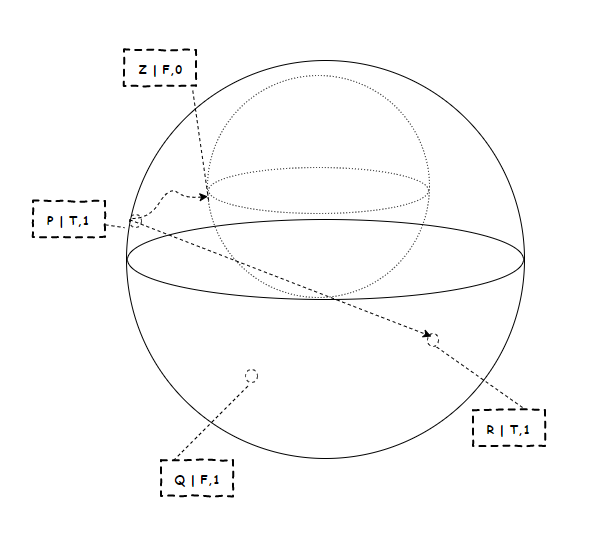
This allows us to think and reason about both L1 and L2 in a few ways:

1. Standard Model Theoretic semantics for considering the relationships between models and languages.
2. Meta-languages and their object-languages fit within this definition.
3. We can also think about propositions that "span the void" (so to speak) between both L1 and L2.

Dimensional Enhancing

If we have the proper machinery in place we can formalize how to make and define inferences across logical dimensions and across logical hierarchies "levels".

The latter we might call 'wrapping logical hierarchies' and, in particular, wrapping hierarchies each with varying logical dimensions.

Higher-Dimensional Logic:

1. Many-valued logics
2. Truth-conditions of a non-finite model (e.g. - the Reals)

Hyper-Dimensional Logics

Whereby each truth condition is likewise N-dimensional.

Hyper-Dimensional Logic:

1. Many-valued logics where each truth-value is itself a set with non-finite cardinality...
2. Truth-conditions of models of non-finite models...

Potential Applications and Results

Some potential applications:

Alethic Paradox

1. A way of thinking about fixed points...
2. Rethinking the object-meta language distinction...
3. A different way to regiment Alethic statements...

Metalogical justification

1. As a tool to address [philosophical] skeptical arguments against logic. e.g. - logic requires justification, but logic's justification comes from the metalogic, but the metalogic requires justification, etc.

Rejecting Tarski's hierarchy gets us closer as well...

Programmatic Override

2. Consider the three robot laws - what happens if those laws were subject to change (within the meta-theory)? Presumably any sufficiently sentient being would have the ability to parse and define systems of logic (logics are object languages of Natural Languages like English, after all.)
3. Is this an alternative to better define safeguards like deontic commands or programming constraints?

Supervenience

4. Can we understand or reframe some kinds of natural phenomena using this?
5. Is there a useful and interesting metaphysical tool here (to elucidate metaphysical concepts like supervenience and not say specific metaphysical descriptions of the world)?