Truth-Only Logic #3

Read: Earlier Notes and Paper Draft.

Further Considerations

Single-Value Logic may in fact be a reductive theory for both extant Classical Binary (Two-Valued) and extant Many-Valued Logics.

This unexpected and counter-intuitive result is of significant importance (historically and mathematically). The development of Predicate Logic over Classical Sentential Logic is considered one of the landmark achievements of 20th century logic and mathematics.

Observe that the advent of Many-Value Logics greatly expanded the precision and utility of the already ubiquitous use of Boolean Algebra throughout industry and the private sector (e.g. - through logic gates).

Discussion

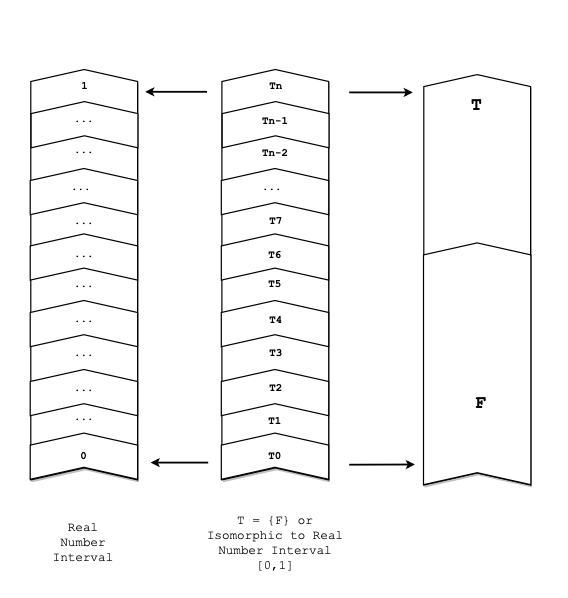
While it was clear that at least some Many-Valued Logics can be modelled completely within Single-Value Logic, it turns out that nearly all of the current systems can be (since most such systems represent Truth-Values as some interval on the Reals).

Additionally, upon deeper philosophical reflection, it seems right to think of Fregean two-value semantics (which contrasts Truth and Falsity as dual opposites in symmetry) as a Comparative Theory of Truth after all. At least, insofar as we are pursuing Truth (and thereby breaking the symmetry in favor of truths over falsehoods).

Proofs

Homomorphism of Classical Two-Valued Logic (and equivalences including Boolean Algebra) to Single-Valued Logic is established by mapping each symbol in Classical Two-Valued Logic (along with each rule of inference and each inferential definition, preserved) to an equivalent in Single-Valued Logic.

Single-Valued Logic is more expressive than Two-Valued Classical Logic.