Thinking Notation #3
Read: previous entry
Semantics
Semantics for Thinking Notation can be constructed from two syntactically valid Thinking Notion streams of thought (or, thinking sequences).
Recovering Boolean Algebra
Deriving the semantics for Boolean Algebra from Thinking Notions is a straightforward affair. We can compare two thinking sequences (henceforth, sequences) and evaluate them as True or False if they are identical or not.
Recovering Predicate Calculus
Using the Grouping syntax specified previously, we can also construct the necessary resources for the semantics of Predicate Calculus.
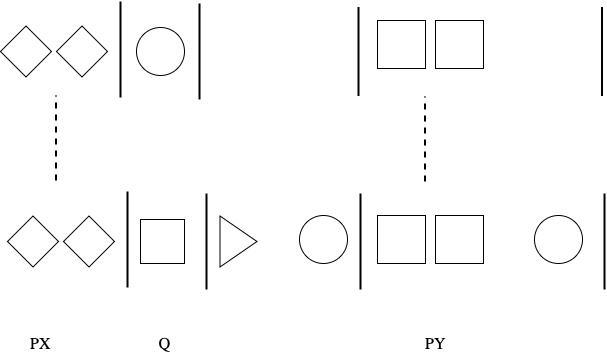
We can also substitute the traditional First Order syntax as needed (by associating constants, variables, and quantifiers with items in a thinking sequence).
Semantics of Semantics
Sequences of sequences can also be formed.
This can be used to represent familiar model-theoretic model classes or sets of interpretations.
As a Higher-Dimensional Logic
Naturally, sequences of sequences can be used to construct dimensional and higher-dimensional logics.
- Thinking Notation
- Thinking Notation #2
- Thinking Notation #3
- Thinking Notation #4
- Thinking Notation #5
- Thinking Notation #6
post: 11/26/2019
update: 4/2/2020