On Connection Theory

Brief update:

1. I previously began an effort to cogently defend Eliminative Ontic Structural Realism (EOSR) - the motivation is clear (for the proponent of EOSR to debate the viability of their project using First Order Model Theory and its conceptions of relations is just to concede the point in the first place).
2. It was pointed out to me at that time that there were some (perhaps superficial) parallels between what I was doing and String Theory. I want to talk a bit more about this below.
3. More significant progress was made recently.
4. I've begun to connect another side-project (called Thinking Notation) to Connection Theory. It turns out there are some interesting parallels.

Why Connection Theory?

I describe this a little more elegantly in the paper draft and I won't dabble much further with it here.

The explicit aims (from the draft) include:

1. Philosophical: To supply an objectless ontology for sensibly discussing ontologies that are purely relational in nature – that is which lack talk of any objects. Crassly, it’s not that “everything’s related” it’s the perspective that “there are only interconnections, no things.” Whether that be read metaphysically or not (here it is not).
2. Current: To capture and express known ontological concepts that are presently essential to mathematical activity: sets, ordinals, functions, mappings, categories...
3. Posthuman: To lay the groundwork for a (posthuman), noun-less, proto-language.

Not a language that is without symbol (body language or gestures will suffice) but that which whose meanings are devoid of the Predicate Subject/Object schemata (the denial of which was asserted to be primary in logic by Bradley and is common in certain Buddhist lines of thinking) and which lack the kind of referential assumptions that engender philosophical angst.

The answer to Wittgenstein might be that human language, so conceived, is powerless to reveal. But like Heidegger observed, technology reveals – and herein, the aim of a new technology of and in language.

4. Ontological: To rigorously define the conceptual equivalent of a ‘set’ to Set Theory or a ‘category’ to Category Theory. To define a fundamental “building block” (as it were) of a new way of viewing existing and novel mathematical theories.
5. Exploratory: To layout a system of axioms which may be selected, rejected, or expanded to see what results. Are there new kinds of mathematical entities that are free of the constraints of Set-Theoretic Foundations (particularly functions)?
6. Agnostic: It is not eliminative–this is not an attempt to dislodge other systems of thinking but to supplement them. I take a methodologically non- foundationalist and broadly pluralist approach within mathematics (I proclaim no metaphysical allegiances – operating neither as a Logicist nor a Formalist. No claim to Platonistism, etc.).
7. Clarificatory: To illuminate the implicit and largely abstracted assumptions that guide functional analysis throughout mathematics today. We talk about functions as if one were to talk about decimal numbers but only by counting in groups of 10 or say constantly rounding to the nearest integer. There is a degree of obfuscating approximation that upon illumination may pioneer some great new work.
8. Univalent Foundations: To link results here to emerging results in Univalent Foundations. Particularly with respect to invariance, isomorphism, equivalence, and identity.
9. To approach a fuller and more complete understanding about how diagramming (itself) works for any theory it can recover. Along the way, to depict more clearly several representation theorems. To rigorously define a universal mechanism to unite diagramming in multiple areas (that are mostly done informally) but that are also nearly indispensable in their areas of inquiry.
10. (Potentially) Negative: If the findings here are partially or fully incorrect (or wrong in some way), it’s useful to understand why. The arguments I give seem compelling to me, enough to warrant my attempting this effort. Illuminating what’s wrong here might be even more valuable than a positive assertion about what’s new or right.

Thinking About String Theory

String Theory is a physical mechanical system that describes subatomic particles as they move through and interact with each other in spacetime.

String Theory addresses several longstanding and important problems in physics. Here, we'll focus on the attempt to replace points as the primary entity of interest when we think about physical space.

I've long expressed my dissatisfaction with points and dots as guiding metaphors in political philosophy, geometry, and mathematics as a whole. Part of this motivation was inspired by the works of String Theorists like Brian Greene.

Here are some interesting parallels:

1. My first pass at Relational Bundles made no distinction between open and closed relations (nor even directed ones).
2. Graph Theory presupposes two categories: a set of edges and a set of vertices that are then combined to form the familiar "lattice-style" diagrams that are used. Here, Relational Bundle Theory and Graph Theory diverge (although they share some superficial diagramming features).
3. Diagrams are used heavily in chemistry (Lewis Diagrams for covalent bonds) and physics (Feynman Diagrams) and I wanted to create a system flexible to unite and formalize diagramming techniques since it (diagramming) is used quite formally throughout math (Commutative Diagrams) and science today (though the diagramming assumptions themselves remain largely unformalized - a strange state of affairs).

Later attempts to address shortcomings with the original proposal and advance it to a higher level (in some sense), resulted in a clearer distinction between kinds of connectors (which became formalized):

1. Connectors share the same features as the "building-blocks" of Relational Bundle Theory - entities that have the ability to be "interlocked", "combined", "stuck", or "fit into" one another. So, there not both relata (objects, properties, relations) and relations (relations) but one kind.
2. Like many String Theorists presupposed (and whom I was directly inspired by), there's an obvious need for some kind of relational entity that can "point" at itself (e.g. - automorphisms, isosymmetries, identity, etc.). Hence, a need for both open and closed connectors. This parallels how strings can be in one of two "states": open and closed but for entirely different reasons. Strings can also take on branes and spaces themselves (which connectors, so conceived, cannot).
3. Both strings and connectors play "building-block" or "fundamental ontological unit" roles for their theories. However, String Theory is a physical theory that uses sets (it presupposes them) to formalize how the mechanics of strings work. Connection Theory is an alternative to Set Theory. Its role is to be a universal, relational, language that standardizes notions about diagramming while being individually interesting as a mathematical theory (read the preceding section for some of these more explicit aims).

Syntax

Note: the syntax diagram above shows several equivalent ways the marks can be written or drawn. The choice of notation is largely irrelevant.

The two relevant, operative, notions are the idea of a syntactic mark (also a fundamental, but relational, ontological unit) called a connector depicted as a curved line (originally called relations) with two ends (called legs or slots) because it reminded me of a side-desk, horseshoe, key-chain, or stand.

Incidently, it turns out that there's in fact a well-known mathematical object called a Pair of Pants - https://en.wikipedia.org/wiki/Pair_of_pants_(mathematics) used to describe certain configurations of Strings: https://arxiv.org/pdf/1310.4319.pdf page 13 - so this seems less an arbitrary choice on my part.

1. A depicts the original Relational Bundle concept.
2. BI and BII depict the next iteration (now, properly called Connection Theory) where the notion of a Leg has been replaced with the box operator (which can be entirely omitted but for convenience sake is useful to depict - not to be confused with the box operator of Modal Logic).
3. CII depicts how directedness can be reduced to a sequence of connector operations. So, no fundamental arrows are needed here. Again, just the single mark (the connector)!
4. D depicts how some of Thinking Notation's original symbols can be replaced with a single syntactic stroke. A thinking sequence can be constructed entirely out of connectors!

From page 15 of the current draft: I note one some of the formal linguistic differences between lambda calculus variables and the original box operator. Note: I use slightly abbreviated Lambda Calculus notation above (retaining the implication arrow). See page 106: https://www.cis.upenn.edu/~cis511/notes/proofslambda.pdf for more.

Thinking About Thinking Notation

It turns out that:

1. Thinking Notation can be used to describe all operations of Connection Theory.
2. Thinking Notation can be reduced to a single syntactic mark (the connector).

Some further thoughts motivated by considerations from Sign, Identity, Relations.

(From the equivalences established above.)

1. AA - Can the idea of an operation applied to an entity to create a relation be intelligibly applied here? Yes!
2. BB - Can the distinction between the operation stroke and the fundamental syntactic unit be eliminated? Yes!
3. CC - Here, the familiar connector is introduced - that is, it is defined as the output of (or equivalent to) BB.
4. DD - Again, a directed function is constructed from multiple BB marks.
5. EE - Simplifying the diagram to more familiar connector and connectionless connector notation.

This comprises a basic algebra (although one with fewer axioms and constraints than a Ring, Group, or Field).

Set Theory

Reconstructing (recovering) theories in Connection Theory is fairly straightforward. A representation thereom is proven to demonstrate a one-to-one correspondance between a subfragment of Connection Theory to some target mathematical theory:

1. Below, Venn Diagrams are covered (and therefore Set Theory).
2. And, a second, isomorphic, fragment (with familiar elementary inclusion relations).

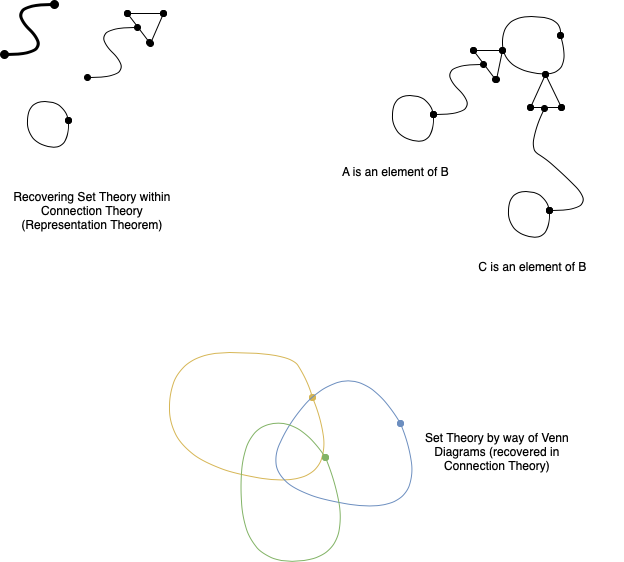
Representation Theorems

Surprisingly, I was probably more aligned with Tennant early on:

"In some cases, it is claimed, a picture alone is a proof (Brown 1999: ch. 3). But that view is rare. Even the editor of Proofs without Words: Exercises in Visual Thinking, writes “Of course, ‘proofs without words’ are not really proofs” (Nelsen 1993: vi). Expressions of the other extreme are rare but can be found:"

He continues:

“[the diagram] has no proper place in the proof as such. For the proof is a syntactic object consisting only of sentences arranged in a finite and inspectable array. (Tennant 1986)”

The article concludes:

Between the extremes we find the view that, even if no picture alone is a proof, visual representations can have a non-superfluous role in reasoning that constitutes a proof."

I found the following to be particularly of interest:

"What about Tennant’s claim that a proof is “a syntactic object consisting only of sentences” as opposed to diagrams?"

From: https://plato.stanford.edu/entries/epistemology-visual-thinking/#VisThiPro

I now clearly disagree - diagrams, that are formally accepted (that is accepted as being formal proofs), are clearly syntactic whether or not they are accepted as free-standing proofs (on their own) is an independent question.

In such circumstances, diagrams are used since they exhibit certain formal properties (e.g. - homomorphic or isomorphic) that can reasonably modeled pictorially (or otherwise).

Read:

1. https://www.ucl.ac.uk/philosophy/people/emeritus-professors/marcus-giaquinto
2. Limits of diagramming in proof: https://academic.oup.com/philmat/article-abstract/19/3/281/1387231?redirectedFrom=fulltext

Note that the scope of Connection Theory is not epistemic (foundational), it is not intended to justify various proof-theoretic methods but to help formalize their use when and where they are presently used (whether alone or in addition to non-diagrammatic means). In that sense, it is "foundational".

Another interesting and non-trivial objective arises as well: representation itself may be easier to discuss and describe.

Currently it’s a somewhat opaque term in philosophy and what we can describe of it is usually cashed out in one or more related kinds of relations:

1. Isomorphism
2. Correspondance
3. Similarity

These however, when they are equally formalized, tend to descend further into like relations:

1. 1-to-1 mapping
2. Bijective mapping

In such investigations, hands are eventually waved and relations of one kind of another are assumed to be primitives!

I am not a foundationalist (with its metaphor of pyramid). So these concerns do not, to me, invite skeptical worries.

I also think that viewing all things as kinds of language systems (well-defined, combinatorial, processes) aids us to move forward past some of the conceptual murk that beguiled thinkers in the past when thinking about representation (category mistakes, etc., sense data, “objectivity”, “externalism” - note this is not say that these are not meaningful in some sense but that the bulk of work here does not depend on those problematic and likely circular concepts).