On Connection Theory #2

Additional comments.

Purely Relational Semantics

Not to be confused with the following:

1. Relational database languages.
2. Functional programming (although this is closer in spirit).

SQL, for instance, isn't purely relational - its name indicates that specific objects (atomic ones at that) are related to each other via rows, columns, foreign keys, joins, and so on. To confuse SQL or Relational database languages with structuralism is to commit the Fallacy of Overnaming - to try to understand the meaning of a concept purely on the basis of its name.

(Purely) Relational semantics has some interesting features. For starters no linguistic item need be atomic. First-Order Predicate Calculus is grounded by Objects which in turn ground Predicates and Relations (via their Extensions). A purely relational semantics seems to imply that no linguistic item is defined independently of the rest.

Under what conditions does the above property give rise to the following:

1. Semantic Packing: the quantified meaning of expression (the number of distinct meaning units or some equivalent) is both N and N+1.
2. The Propositional Depth of an expression is both N and N+1 such that each proposition expresses a unique non-transparent meaning.

Would the above give rise to hypercomputation through language alone? Granted, I've couched the language above in terms of traditional set-based ordinals, etc.

Some Related Notions

1. Pair of Pants: https://en.m.wiktionary.org/wiki/pair_of_pants
2. Young Diagrams: https://math.ucr.edu/home/baez/twf_young.pdf

Abstraction

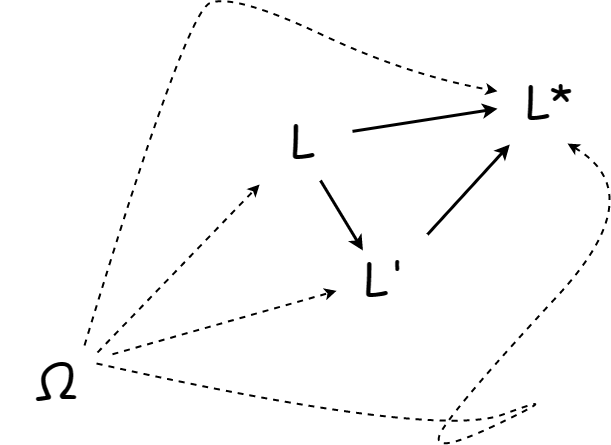
To be able to retain all of some language L while obtaining some new language L* such that:

1. The Semantics of L to L* is one-way/non-symmetric.
2. That L* is not reducible to L semantically.
3. We don't know what L* is yet (so it can't be a starting point for our inquiries).

We'd likely use "abstraction" and dig deeper than both L and L* to find something that can express or write L and also L*.

Boundary Phenomena at the Transition Barrier

The one-way nature of some language L to L* mapping implies that there's a natural barrier between the two.

Crossing that "transition barrier" from one language into the next is one-way. What would that entail precisely?

1. Sudden jumps to non-spatial vocabularies, non-procedural languages, novel entities that cannot be constructed in L?
2. Sudden shift in the accuracy, detail, or precision of thinking since L* might be unencumbered by the metaphysical and language baggage of L?

Is this akin to Kuhn's semantic incommensurability (from whence the term/phrase "paradigm shift" comes from)?

Or is this akin to mystical revelation and/or platonist intuition?